01 - Złożoność obliczeniowa algorytmów
Systemy Wbudowane i Przetwarzanie Brzegowe
Politechnika Poznańska, Instytut Robotyki i Inteligencji Maszynowej
Ćwiczenie laboratoryjne 1: Złożoność obliczeniowa algorytmów
Powrót do spisu treści ćwiczeń laboratoryjnych
Analiza złożoności obliczeniowej algorytmów
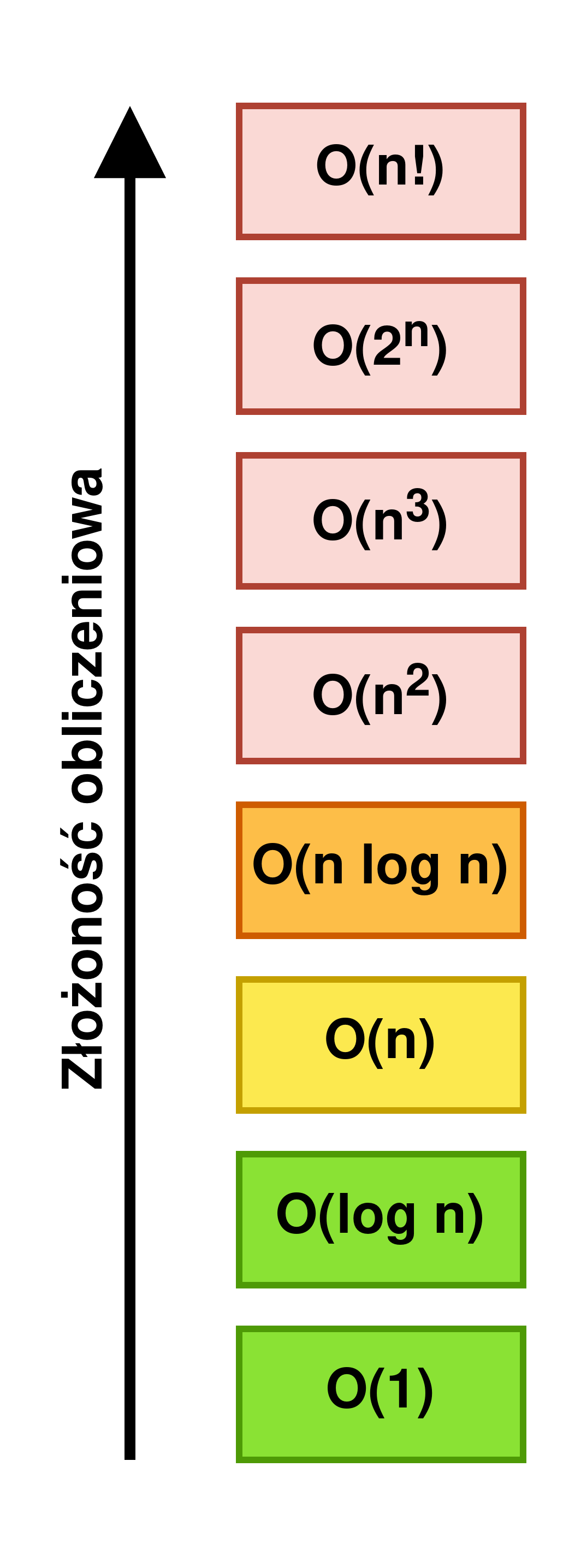
Wydajność algorytmu obejmuje wiele składowych takich jak np. czas wykonywania, zajętość pamięci, wykorzystanie CPU. Złożoność obliczeniowa jest jednym z najważniejszych czynników, które należy uwzględnić podczas projektowania algorytmu. Jest ona określana jako liczba operacji, które muszą zostać zrealizowane, aby wykonać algorytm. Złożoność obliczeniowa jest zwykle określana przy pomocy notacji duże O, która jest zdefiniowana jako asymptotyczne tempo wzrostu, czyli miara określająca zachowanie wartości funkcji wraz ze wzrostem rozmiaru jej danych wejściowych. Notacja ta określa tempo wzrostu w najgorszym scenariuszu, czyli maksymalną liczbę operacji, które muszą zostać wykonane.
Zadanie 1. Zaimplementuj metodę, która zwraca sumę pierwszej wartości n-elementowej listy podniesionej do drugiej potęgi oraz ostatniej wartości podniesionej do trzeciej potęgi. Zbadaj złożoność obliczeniową algorytmu poprzez przygotowanie wykresu czasu wykonania algorytmu w zależności od n, do pomiaru czasu wykorzystaj perf_counter z biblioteki time. Wykonaj eksperymenty dla n od 2 do 50. Porównaj wyniki z teorią.
Zadanie 2. Zaimplementuj funkcję obliczającą sumę liczb naturalnych od 0 do n. Zbadaj złożoność obliczeniową algorytmu poprzez przygotowanie wykresu czasu wykonania algorytmu w zależności od n, do pomiaru czasu wykorzystaj perf_counter z biblioteki time. Wykonaj eksperymenty dla n od 2 do 50. Porównaj wyniki z teorią.
Zadanie 3. Zaimplementuj algorytm sortowania bąbelkowego dla losowej n-elementowej listy. Zbadaj złożoność obliczeniową algorytmu poprzez przygotowanie wykresu czasu wykonania algorytmu w zależności od n, do pomiaru czasu wykorzystaj perf_counter z biblioteki time. Wykonaj eksperymenty dla n od 2 do 50. Porównaj wyniki z teorią.
Zadanie 4. Zaimplementuj metodę zwracającą n-ty element ciągu Fibonacciego. Zaimplementowana funkcja powinna korzystać z rekurencji. Zbadaj złożoność obliczeniową algorytmu poprzez przygotowanie wykresu czasu wykonania algorytmu w zależności od n, do pomiaru czasu wykorzystaj perf_counter z biblioteki time. Wykonaj eksperymenty dla n od 2 do 40. Porównaj wyniki z teorią.
Zadanie 5. Zaimplementuj algorytm wyszukiwania indeksu elementu w liście przy pomocy drzewa binarnego. Zwróć uwagę, że przedstawiony algorytm wymaga wcześniejszego posortowania wejściowej listy elementów. Zbadaj złożoność obliczeniową algorytmu poprzez przygotowanie wykresu czasu wykonania algorytmu w zależności od n, do pomiaru czasu wykorzystaj perf_counter z biblioteki time. Wykonaj eksperymenty dla n od 2 do 50. Porównaj wyniki z teorią.
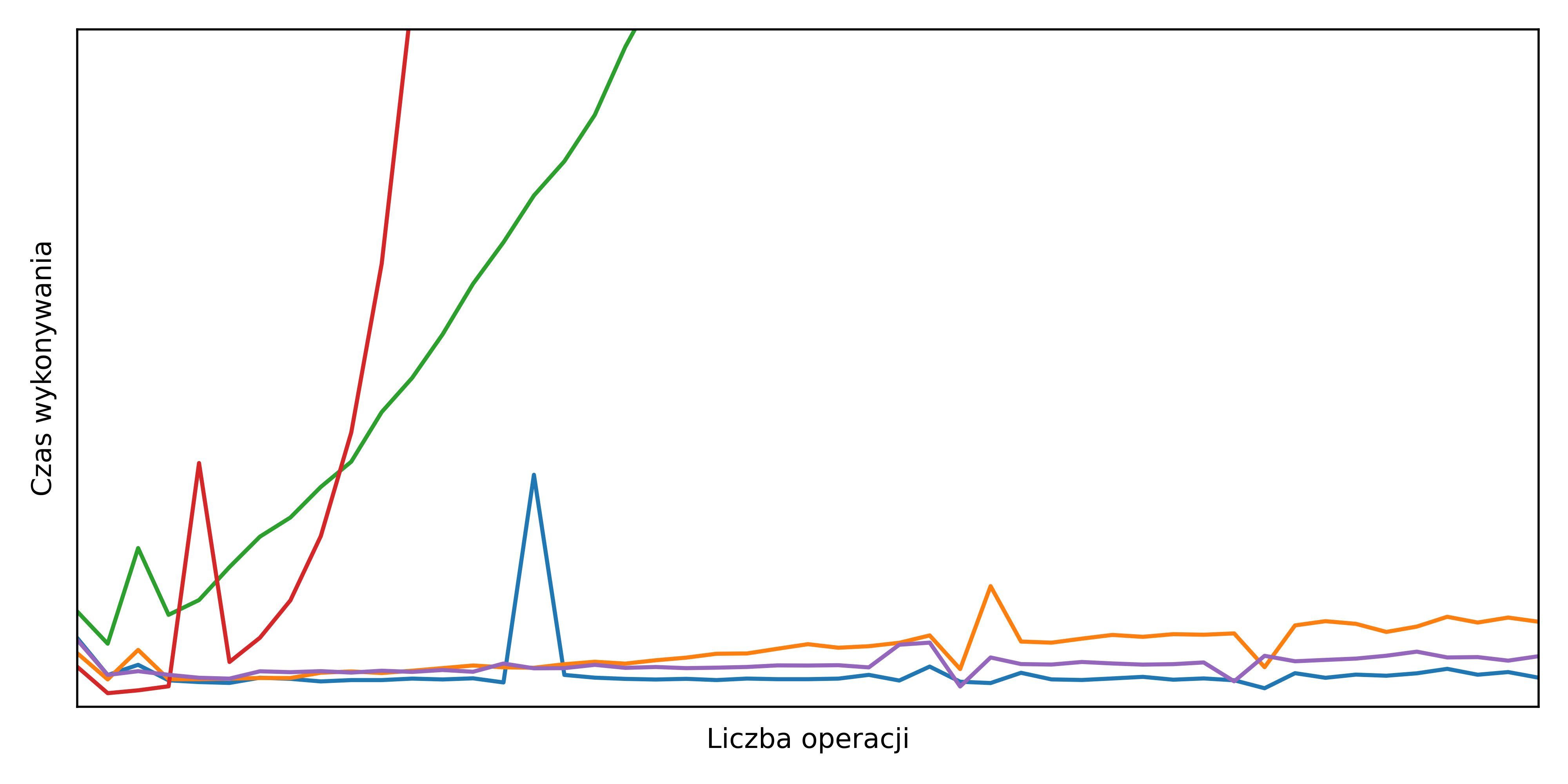
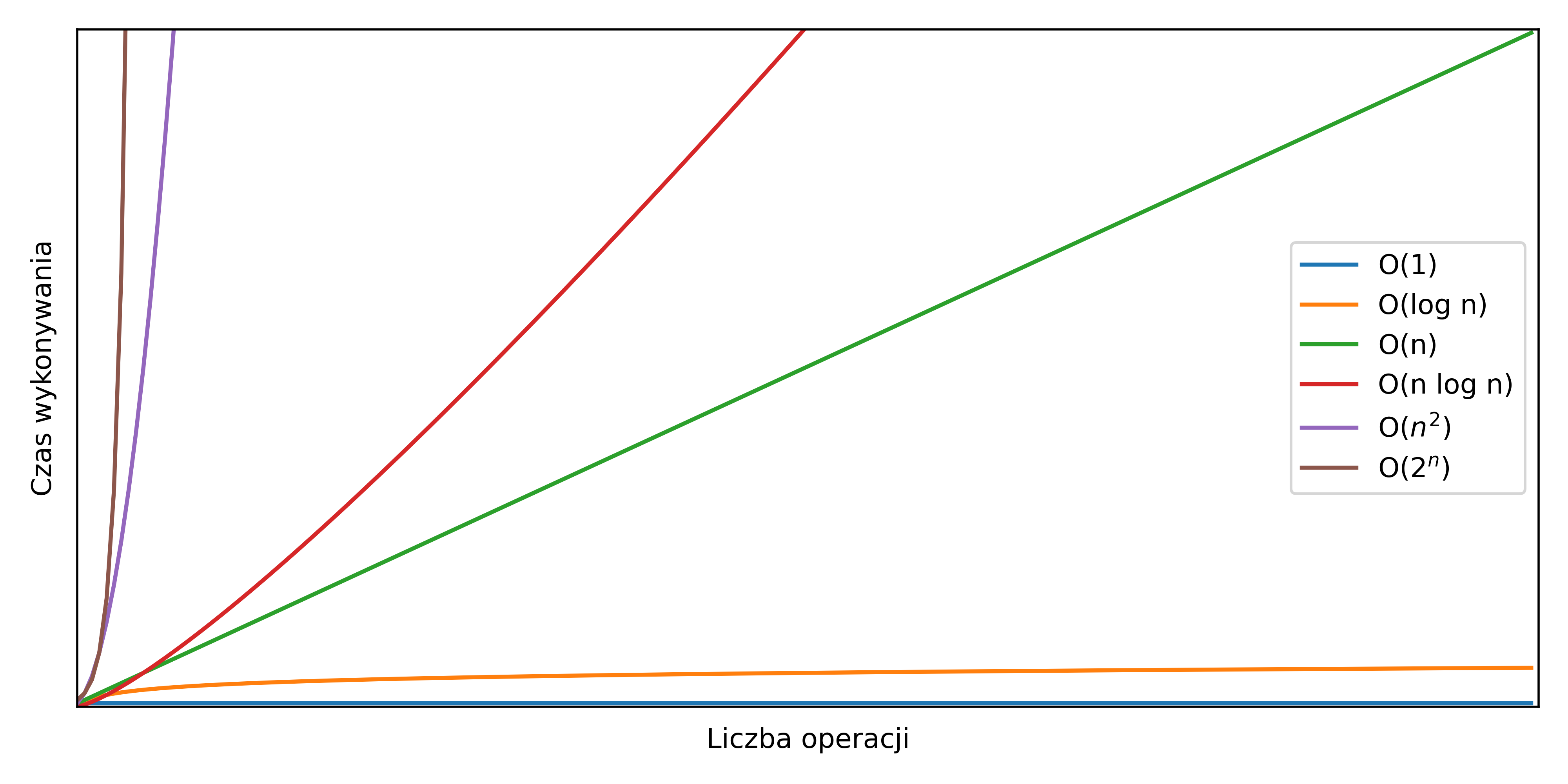
Zadanie 6. Przedstaw powyższe wyniki w postaci
wspólnego wykresu i porównaj z poniższym grafem. Na podstawie
charakterystyki przebiegu określ złożoność obliczeniową w postaci
notacji O i dodaj jako etykiętę do wykresu (np. poprzez parametr
label w funkcji plot z pakietu matplotlib.pyplot).